Soal Persamaan dan Pertidaksamaan Rasional dan Irasional

Nama: Salma Rasikha

Kelas:  X IPS 3

Absen: 30


PERSAMAAN DAN PERTIDAKSAMAAN RASIONAL

~PERSAMAAN

Identifikasi fungsi yang diberikan oleh grafik pada gambar di bawah, lalu pakailah grafik tersebut untuk menuliskan persamaan fungsi tersebut. Anggaplah |a| = 1

asimtot

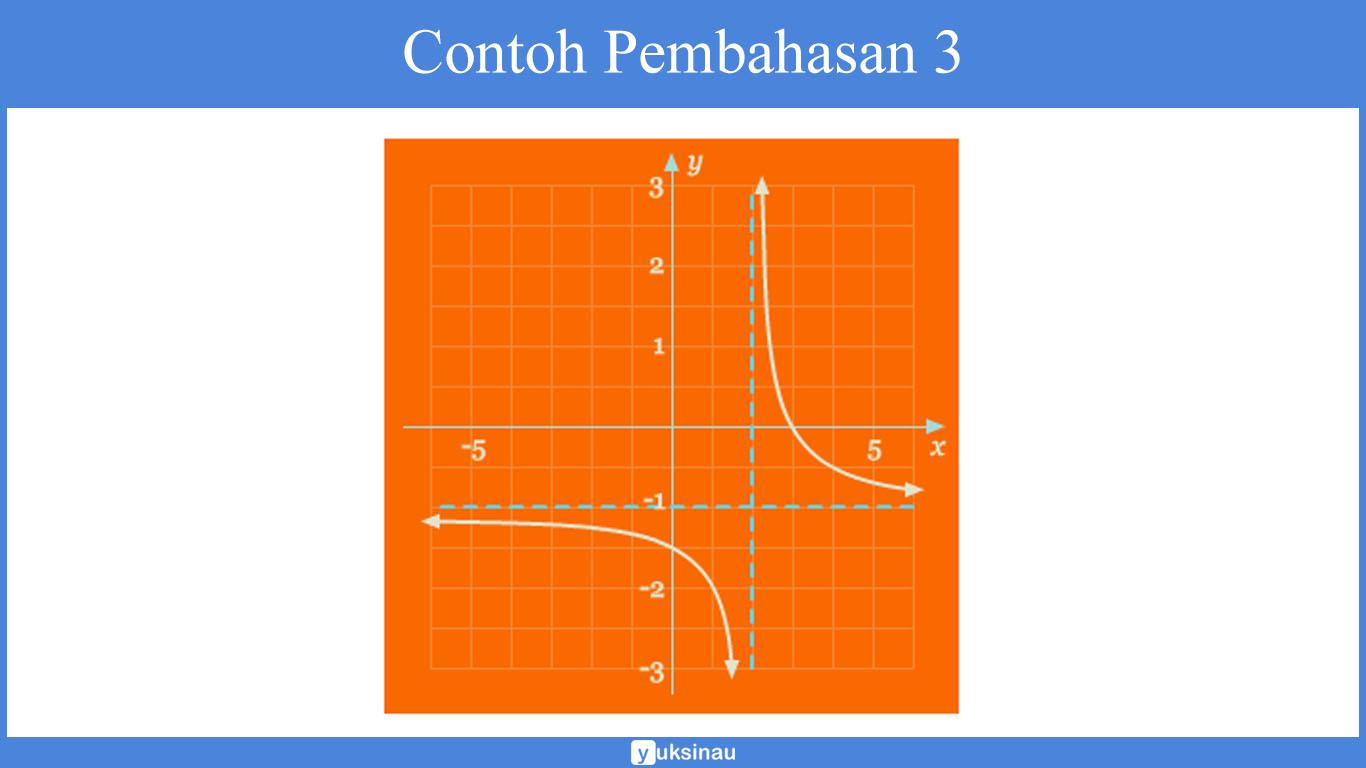
Pembahasan dari grafik di atas, dapat kita ketahui bahwasannya grafik tersebut adalah pergeseran dari fungsi y = 1/x ke kanan sejauh 2 satuan. Serta bergeser ke bawah sejauh 1 satuan.

Sehingga asimtot horizontal serta vertikal dari grafik di atas secara berturut-turut yaitu y = –1 dan x = 2. Maka dari itu, persamaan dari grafik di atas yaitu:

pergeseran dari fungsi y

yang mana adalah bentuk dari pergeseran fungsi y = 1/x.

~PERTIDAKSAMAAN

  1. Tentukan himpunan penyelesaian dari  :

Jawab:

Pembuat nol adalah
x − 3 = 0  ⇒ x = 3
x + 1 = 0  ⇒ x = −1

Syarat :
x + 1 ≠ 0  ⇒ x ≠ −1

Untuk interval x < −1, ambil x = −2 : 

Untuk interval −1 < x ≤ 3, ambil x = 0 : 

Untuk interval x > 3, ambil x = 4 : 

 Sebab pertidaksamaan bertanda “≥”, maka daerah penyelesaiannya berada pada interval yang bertanda positif (+).

Yaitu: HP = {x < −1 atau x ≥ 3}


PERSAMAAN DAN PERTIDAKSAMAAN IRASIONAL

~PERSAMAAN
1. tentukan nilai x yang memenuhi persamaan irasional √x²-9 = √x+3
Syarat persamaan irasional yaitu:
• x²-9≥0 atau x²≥9 --- x≤-3 atau x ≥3.
• x+3≥0 atau x≥-3.
Kita lihat syara pertama x ≤-3 dan yang kedua x≥-3 jadi syarat yang berlaku adalah x=-3 dan x≥3.
Setelah itu kuadratkan kedua ruas persamaan irasional sehingga di dapat:
• (√x²-9)²=(√x+3)²
• x²-9=x+3
• x²-x-9-3=0
• x²-x-12=0
• (x-4) (x+3)=0
• x=4 atau x = -3
Berdasarkan syarat kedua nilai x memenuhi sehingga jawaban soal ini adalah x = -3 dan x = 4.

~PERTIDAKSAMAAN
1. Tentukan himpunan penyelesaian dari pertidaksamaan irasional √x-5<2
Untuk menjawab soal ini kita tentukan terlebih dahulu syarat agar pertidaksamaan irasional yaitu:
• x-5≥0
• x≥5
Selanjutnya kuadratkan kedua ruas pertidaksamaan irasional sehingga di dapat:
• (√x-5)² <2²
• x-5<4
• x<4+5 atau x<9
Lalu buat garis bilangan untuk menentukan irisan antara syarat x≥5 dan x<9.
Berdasarkan garis bilangan maka himpunan pertidaksamaan irasional adalah 5 ≤ x < 9.


Postingan populer dari blog ini

LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

Gambar
Nama: Salma Rasikha Kelas: X IPS 3 Absen 30 LUAS SEGI-n BERATURAN Luas Segi n Beraturan   Pada segi n beraturan Setiap segi n beraturan bisa kita bagi menjadi n buah segitiga yang kongruen Setiap titik sudut pada segi n beraturan bisa dilalui sebuah lingkaran, lingkaran ini disebut lingkaran luar segi n. Semuat titik sudut akan dilewati lingkaran (tidak ada yang tertinggal).   Menghitung luas segi n beraturan akan lebih mudah jika diketahui jari-jari lingkaran luarnya Setiap segi n bisa dibagi menjadi n buah segitiga yang kongruen seperti pada gambar di atas. Selanjutnya kita ambil salah satu segitiganya Besar sudut A adalah  Luas segitiga adalah LΔ = ½ .R.R sin A Luas segi n beraturan adalah L n  = n. LΔ Rumus ini merupakan rumus luas segi n beraturan yang diketahui jari-jari lingkaran luarnya.   Bagaimana jika diketahui sisinya ? Pertama kita cari dulu hubungan antara jari-jari lingkaran luar (R) dengan sisinya (a) Dengan aturan cosinus maka a 2  = R 2 ...
Baca selengkapnya

Transformasi Geometri

Gambar
SALMA RASIKHA XI IPS 3 absen 32 Transformasi Geometri Pengertian transformasi geometri Sebelum mengetahui pengertian dari transformasi geometri. Kita jabarkan lebih dulu apa itu arti transformasi dan apa itu geometri. Transformasi berarti perubahan sebuah struktur menjadi bertambah, berkurang atau tertata kembali unsurnya. Sedangkan geometri berarti cabang matematika yang menjelaskan soal sifat garis, sudut, bidang, dan ruang. Berdasarkan dua definisi tersebut transformasi geometri dapat disimpulkan sebagai perubahan bentuk dari sebuah garis, sudut, ruang, dan bidang. Dalam kehidupan sehari-hari, transformasi geometri ini biasanya dimanfaatkan untuk pembuatan karya-karya seni dan desain arsitektur. Jenis-jenis transformasi geometri: Transformasi geometri itu sendiri terdiri dari empat jenis, yaitu translasi, rotasi, refleks, dan dilatasi. Berikut adalah pemaparan lengkap masing-masing jenis transformasi geometri: 1. Translasi (Pergeseran) Translasi atau pergeseran merupakan jenis dari ...
Baca selengkapnya

Tugas Matematika Soal Cerita Dari Persamaan 3 Variabel Dan Penyelesaiannya

Gambar
 Nama : Salma Rasikha  Kelas :  X IPS 3  Absen:  30 TUGAS MATEMATIKA SOAL CERITA DARI PERSAMAAN 3 VARIABEL DAN PENYELESAIANNYA. 1.  Pada hari Minggu Wayan, Candra, Agus dan Akbar membeli perlengkapan sekolah di toko buku “Subur”. Wayan membeli 4 buku, 2 bolpoin, dan 3 pensil dengan harga Rp26.000,00. Candra membeli 3 buku, 3 bolpoin, dan 1 pensil dengan harga Rp21.500,00. Agus membeli 3 buku, dan 1 pensil dengan harga Rp12.500,00. Jika Akbar membeli 1 buku, 2 bolpoin dan 2 pensil, berapakah harga yang harus ia bayar?   Penyelesaian: Misalkan a = buku, b = bolpoin, dan c = pensil   Persamaan matematis untuk: Wayan => 4a + 2b + 3c = 26000 Candra => 3a + 3b + c = 21500 Agus => 3a + c = 12500 Akbar => a + 2b + 2c = ?   Diperoleh SPLTV yakni: 4a + 2b + 3c = 26000 . . . . pers (1) 3a + 3b + c = 21500 . . . . pers (2) 3a + c = 12500 . . . . pers (3)   Adapun metode yang dipilih dalam menyelesaikan SPLTV ini yakni dengan menggunakan ...
Baca selengkapnya